MT-223 ORDINARY DIFFERENTIAL EQUATIONS & FOURIER SERIES
CREDIT HOURS
Theory = 3
Practical = 0
COURSE LEARNING OUTCOMES (CLOs)
| S. No. | CLOs | PLO | Taxonomy |
| 1 | Describe formation of differential equations to explain physical situations | PLO-1 |
Coginitive |
| 2 | Apply appropriate methods to solve differential equations of relevant engineering problems | PLO-2 | Coginitive Level 3* |
COURSE CONTENT
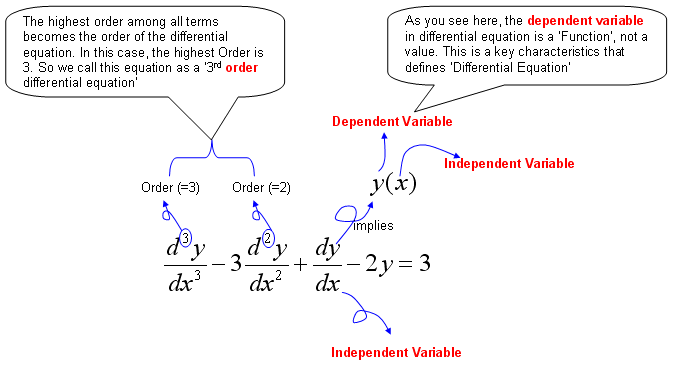
- First Order Differential Equations: Basic concept; Formation of differential equations and solution of differential equations by direct integration and by separating the variables; Homogeneous equations and equations reducible to homogeneous from; Linear differential equations of the order and equations reducible to the linear from; Bernoulli’s equations and orthogonal trajectories; Application in relevant Engineering.
- Second and Higher Orders Differential Equations: Special types of 2nd order differential equations with constant coefficients and their solutions; The operator D; Inverse operator 1/D; Solution of differential by operator D methods; Special cases, Cauchy;s differential equations; Simultaneous differential equations; simple application of differential equations in relevant Engineering.
- Partial Differential Equation: Basic concepts and formation of partial differential equations; Linear homogeneous partial differential equations and relations to ordinary differential equations; Solution of first order linear and special types of second and higher order differential equations; D’ Alembert’s solution of the wave equation and two dimensional wave equations; Lagrange’s solution; various Standard forms.
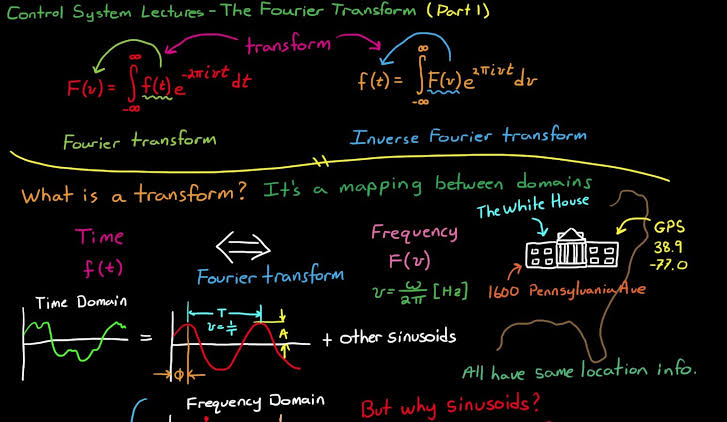
- Laplace Integral & Transformation: Definition, Laplace transforms of some elementary functions, first translation or shifting theorem, second translation or shifting theorem, change of scale property, Laplace transform of the nth order derivative, initial and final value theorem Laplace transform of integrals. Laplace transform of functions t F(t) and F(t)/ t, Laplace transform and inverse transforms, convolution theorem, solutions of ordinary differential using Laplace transform.
- Fourier series: Periodic functions and expansion of periodic functions in Fourier series and Fourier coefficients; Expansion of function with arbitrary periods. Odd and even function and their Fourier series; Half range expansions of Fourier series, “DFT and FFT, Fourier Spectrum”.
RECOMMENDED BOOKS
(01) Advanced Engineering Mathematics by Erwin Kreyszig
(02) Differential Equations by G. Zill
(03) Introduction to Differential Equations by J. Faraw
*For details of Taxonomy Levels CLICK HERE!