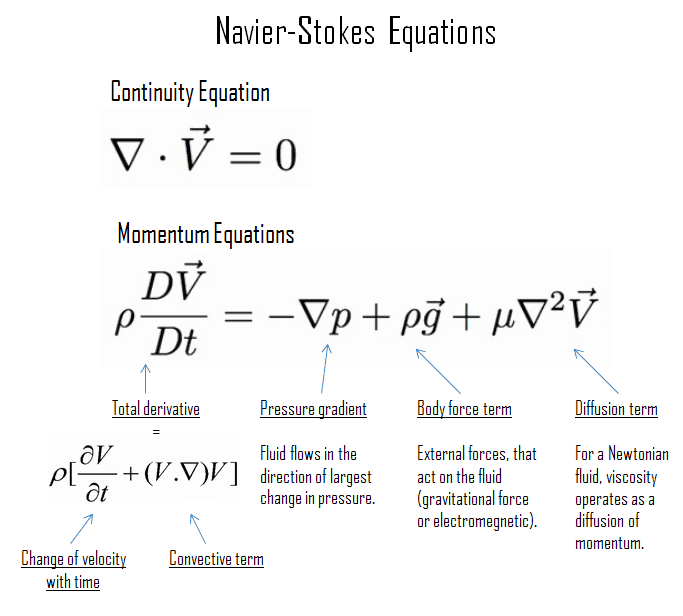ME-574 FLUID DYNAMICS
Credit Hours = 3
COURSE CONTENT
- Introduction: Reynolds transport theorem, Conservation of mass equation, Navier Stokes equation, Energy equation, Dimensionless form of governing equations, Vorticity transport equation
- Exact solutions of Navier Stokes equation: Fully developed flow in a parallel channel and a pipe, Unsteady flow in a tube, Couette flow, steady and unsteady external flows.
- Potential theory: Irrotational flow, stream function / velocity potential approach, examples of potential flow: uniform flow, source, sink and vortex flow, airfoil theory, types of airfoils.
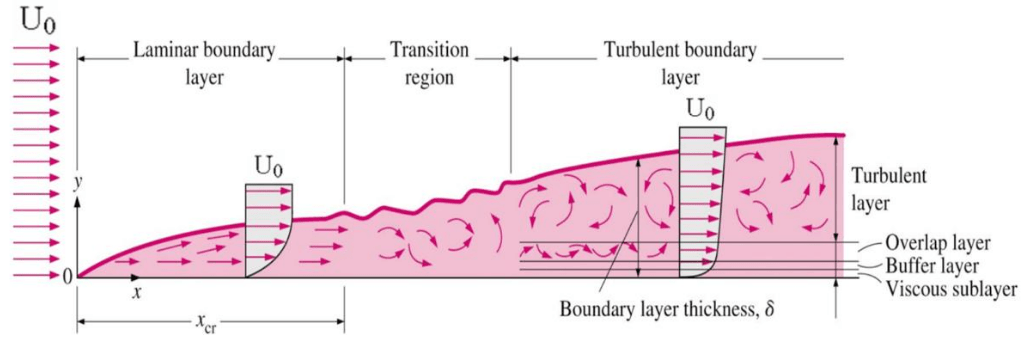
- Laminar boundary layer and hydrodynamic stability: Blasius flow over a flat plate, Momentum integral equations, Separation of boundary layer, Separation and vortex shedding, flow stability, Tollmien Schlichting waves.
- Turbulence: Length scales, spectrums, Energy cascade, Computations of turbulence, RANS, LES and DNS, RANS based models.
- Computational Fluid Dynamics: Classification and application of partial differential equations: elliptic, parabolic and hyperbolic partial differential equations.
- Numerical solution methods: Explicit and implicit methods, Upwind differencing, Power law and hybrid differencing; QUICK scheme, SIMPLE and SIMPLEC algorithm.
- Truncation errors, Round-off errors, Aliasing errors, Verification and validation.
- Implementation of boundary conditions: Numerical treatment of Dirichlet, Nuemann, and mixed type boundary conditions.
- Use of CFD software.
RECOMMENDED BOOKS
(01) Advanced Fluid Mechanics by W. Graebel
(02) Fluid Mechanics by J. Spurk, N. Aksel
(03) Fluid Dynamics: Theory, Computation, and Numerical Simulation by C. Pozrikidis
(04) An Introduction to Computational Fluid Dynamics: The Finite Volume Method by H. Versteeg & W. Malalasekera